לפוסט המקורי באנגלית
עזרו למדריך הזה להגיע ל R > 1:
מה הלאה? .העתיד עם הקורונה, ואיך מנצחים אותה
מה הלאה?
העתיד עם הקורונה ואיך מנצחים אותה
🕐 30 דקות קריאה/משחק
Marcel Salathé (epidemiologist) & Nicky Case (art/code)
תרגום: אשר ברק

והעיקר, אמרו לנו, לא לפחד כלל.

אז נכון, לא צריך לאגור נייר טואלט, אבל יש מקום לקצת פחד בריא. השאלה היא איך משתמשים בפחד הזה כדי להתמודד עם הבעיות של עכשיו ולהתכונן למה שמצפה לנו.

גם אנחנו (Marcel, epidemiologist + Nicky, art/code) מודאגים. לכן הכנו את הסימולטור הזה ואתם מוזמנים להשתמש בו כדי להפוך את הפחד שלכם להבנה:

המדריך הזה (פורסם בתחילת מאי 2020 1) והוא מיועד לתת לכם גם תקווה וגם פחד. כדי לנצח את COVID-19 בדרך שגם תשמור על הבריאות הנפשית והכלכלית שלנו אנחנו צריכים אופטימיות כדי לתכנן תכניות, ופסימיות כדי לתכנן תכניות גיבוי. כמו שאמר Gladys Bronwyn “האופטימי ממציא את המטוס והפסימי ממציא את המצנח.”

נצא לדרך:

החודשים האחרונים

טייסים מתשמשים בסימולטורים כדי ללמוד איך לרסק מטוסים ולצאת מזה בשלום.

אפידימיולוגים משמשים בסימולטרים כדי ללמוד איך להוציא את האנושות בשלום ממגפות.

אז למה לא נבנה לנו סימולטור מגפות מאד מאד פשטני! בסימולטור הזה, אנשים מדבקים יכולים להפוך אנשים פגיעים למדבקים (פגיעים הם אנשים שאין להם חסינות והם גם לא חולים או מדבקים בעצמם כרגע).

(הערת המתרגם: אשמח למשוב מקצועי על התרגום בכלל ועל המונחים הרפואיים בפרט. הכי נח בטוויטר)

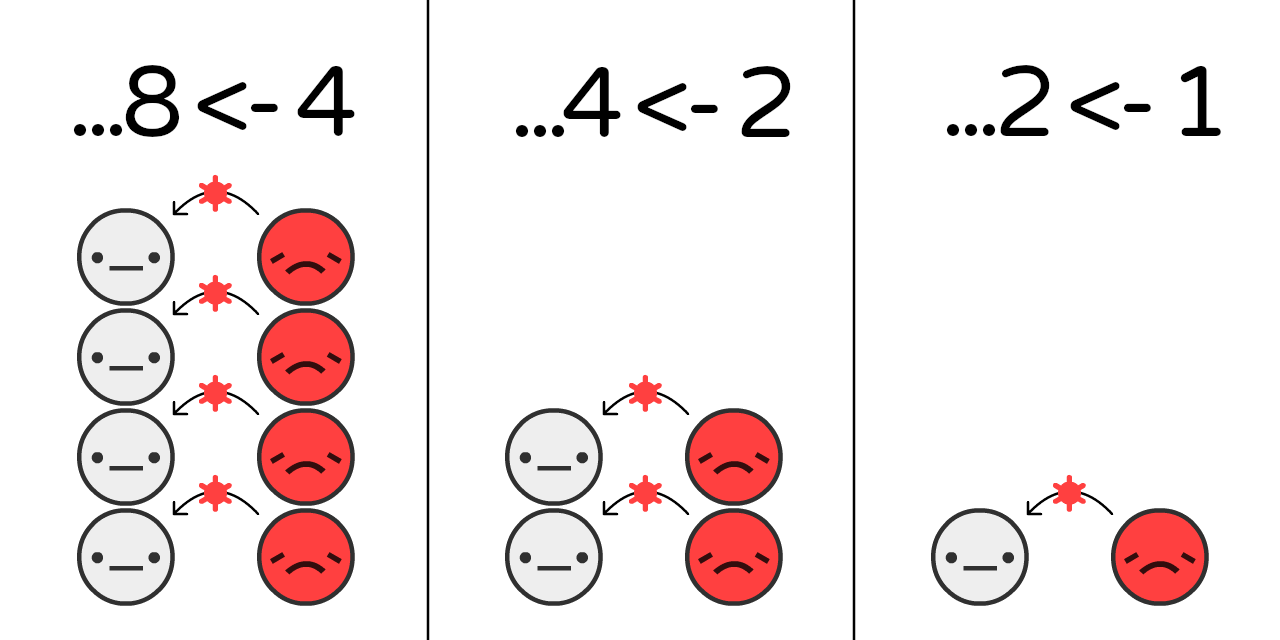
מעריכים שבתחילת ההתפרצות של COVID-19, הוירוס דילג מ ל כל 4 ימים בממוצע2. (כדאי לזכור שיש כאן שונות מאד גדולה)

אם אנחנו מכניסים לסימולטור שלנו “הכפלה כל 4 ימים” ושום דבר אחר על אוכלוסיה שמתחילה עם 0.001% , מה יקרה?

לחצו ‘הפעל’ כדי להתחיל את הסימולציה! תוכלו להפעילו אותה שוב אחרי שתסתיים וגם לשחק עם ההגדרות! (הסתייגויות טכניות: 3)

זה הגידול האקספוננציאלי. מתחיל קטן, ואז מתפוצץ. בהתחלה: “זאת רק שפעת” ואז: “משפעת לא נהיים קברים המוניים בערים גדולות של מדינות מפותחות”.

אבל הסימולציה הזו לא נכונה. גידול אקספוננציאלי, למרבה המזל, לא יכול להמשך לנצח. אחד הדברים שעוצר את ההתפשטות של הוירוס הוא כשלאחרים כבר יש אותו:

ככל שיש יותר מי שהוא נהיה מהר יותר, אבל, ככל שיש פחות , מי שהוא נהיה לאט יותר.

איך זה משפיע על התפשטות המגיפה? בואו נראה:

זו העקומה הלוגיסטית. מתחילה בקטן, מתפוצצת, ואז שוב דועכת.

אבל הסימולציה הזו עדיין לא נכונה. אנחנו מפספסים את העובדה ש אנשים מדבקים בסופו של דבר מפסיקים להדביק. או שהם מחלימים, או שהם “מחלימים” עם נזק לריאות, או שהם מתים.

לשם הפשטות, נניח שכל המדביקים נהיים מחלימים. (רק נזכור שבמציאות חלק מהם מתים) לא יכולים להדביק שוב, ונניח לעת עתה שהם נשארים חסינים לשארית חייהם.

ההערכה היא שעם COVID-19 אתה מדבק למשך 10 ימים בממוצע4 . זה אומר שחלק יחלימו לפני שיעברו 10 ימים, וחלק אחרי.

זה ההפך מגידול אקפוננציאלי - זו עקומה של דעיכה אקספוננציאלית.

עכשיו, מה יקרה אם נעשה סימולציה של עקומה לוגיסטית עם התאוששות?

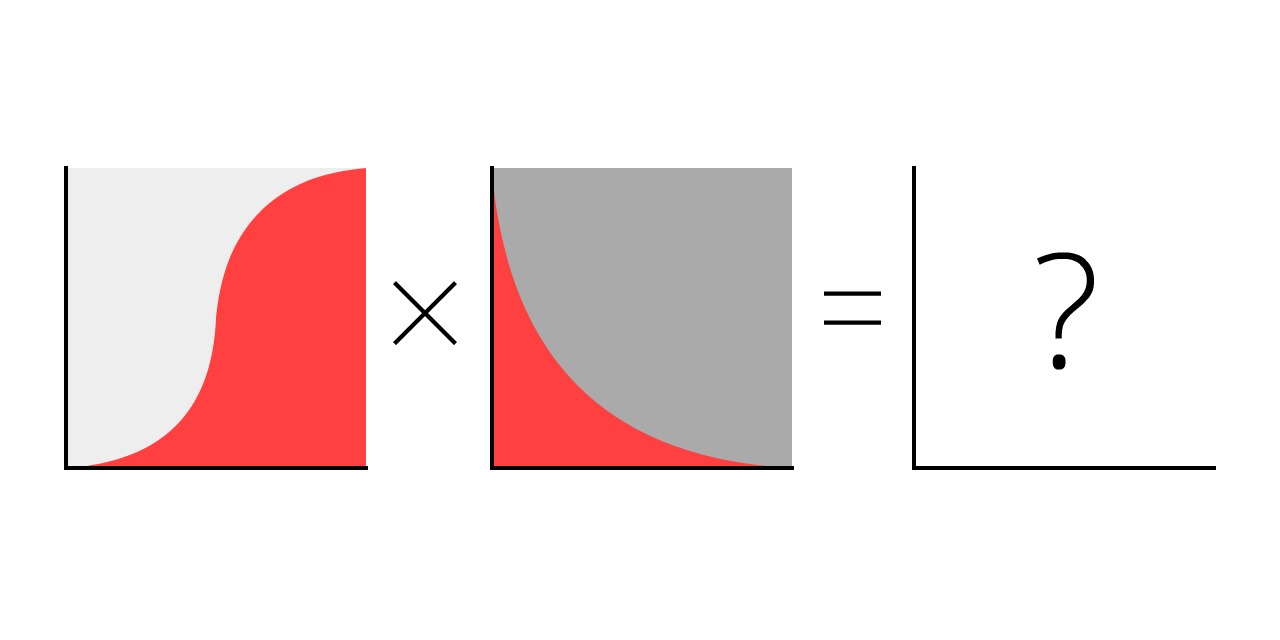
בואו נראה.

העקומה האדומה היא מספר המקרים הנוכחי ,
העקומה האפורה היא סך כל המקרים (נוכחי + מחלימים ), מתחילה בסך הכל ב 0.001% :

וזה המקור של העקומה שאנחנו רואים בכל מקום! זו לא עקומת פעמון, זו לא עקומה שאנחנו מכירים ממקום אחר, אבל זו העקומה שהשתלטה על החיים של כולנו ואותה אנחנו מנסים לשטח!

זה המודל המכונה SIR Model5 (Susceptible - פגיעים; Infectious - מדבקים; Recovered - מחלימים)

הרעיון השני הכי חשוב במבוא לאפידמיולוגיה:

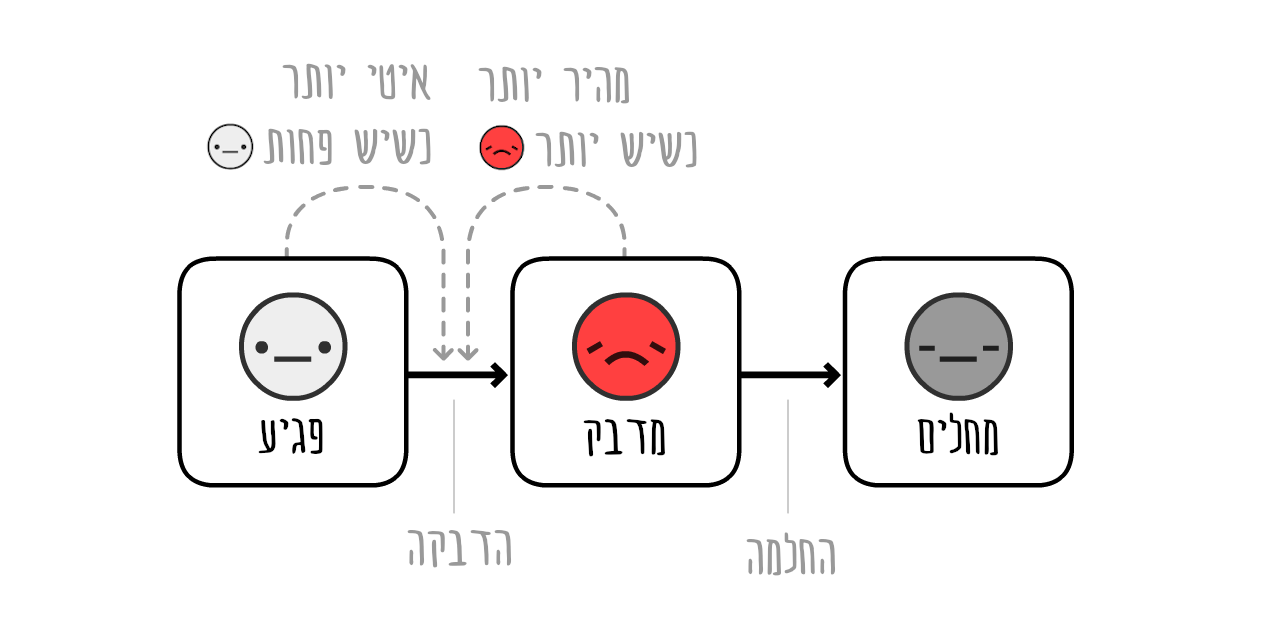
שימו לב: הסימולציות שמשמשות לקבלת החלטות הרבה יותר מורכבות מזה! אבל מודל SIR יכול עדיין להסביר כמה ממצאים מרכזיים, אפילו אם הוא מתעלם מכמה ניואנסים.

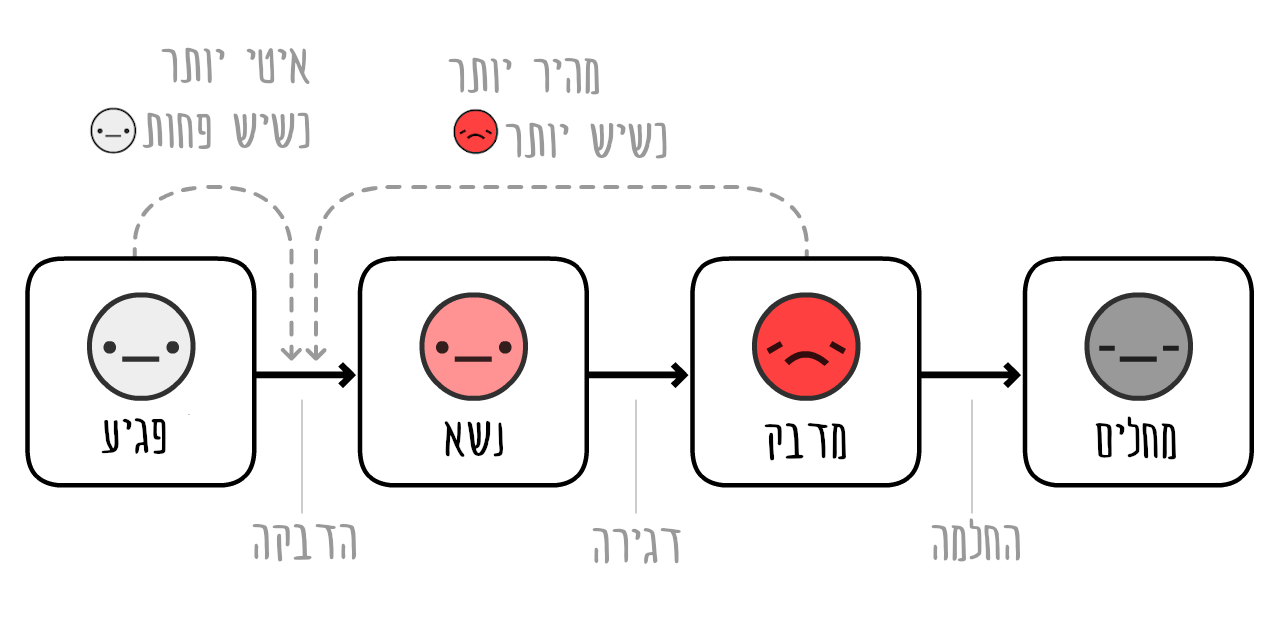
למעשה, בואו נוסיף עוד קצת ניואנס: לפני ש נהיה , הוא נהיה חולה סמוי. זה השלב שבו הוא כבר נדבק בוירוס, אבל הוא עדיין לא מדביק אחרים.

הגרסה הזו של המודל מכונה SEIR Model6 והאות E פירושה “Exposed” . (שימו לב שהמילה Exposed משמשת בשפה היום יומית לתאר מישהו שנחשף לנגיף אבל אולי לא נדבק. כאו הכוונה היא למישהו שנדבק בוודאות אבל עדיין לא מדבק)

ל COVID-19, ההערכה היא שאתה למשך 3 ימים, בממוצע חולה סמוי-אבל-לא-מדבק.7 מה יקרה אם נוסיף את זה לסימולציה?

העקומות האדומה + הוורודה ביחד הן כמות המקרים הנוכחית (מדבקים + חולים סמויים ),
העקומה האפורה היא סך כל המקרים (כמות מקרים נוכחית + מחלימים ):

לא הרבה השתנה. משך הזמן שבו אתה נשאר חולה סמוי משנה את היחס בין -ל-, ומתי כמות המקרים תגיע לשיא, אבל אבל הגובה של השיא הזה, וכמות המקרים הכללית בסופו של דבר, לא משתנה.

למה? בגלל העיקרון הראשון של מבוא לאפידימיולוגיה:

שמסמל את ה “Reproduction number”. המספר הממוצע של אנשים ש מדביק לפני שהוא מחלים (או נפטר).

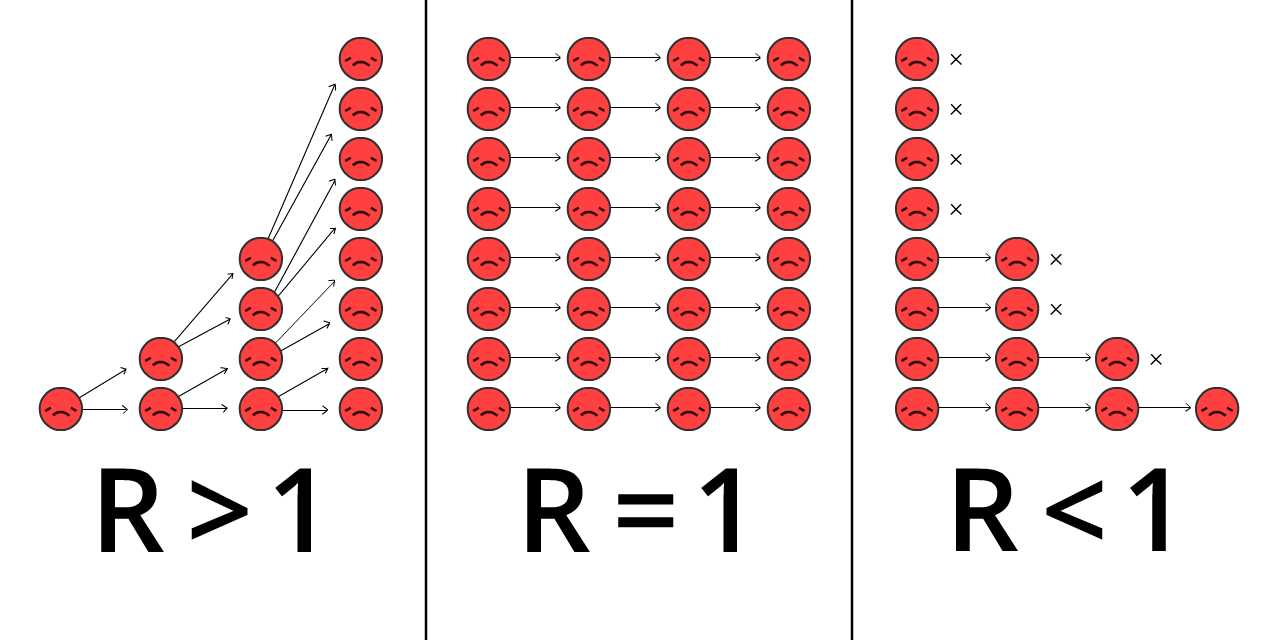
R הוא זה שמשנה את הכיוון של ההתפרצות כשאנחנו מפתחים יותר חסינות או מתערבים במצב בכל מני דרכים.

R0הוא הערך של R בתחילת ההתפרצות, לפני שאנשים התחילו לפתח עמידות ולפני שהתחלנו לנקוט באמצעים לריסון ההתפרצות. R0 משקף טוב יותר את העוצמה של הנגיף עצמו, ועדיין הוא עשוי להשתנות ממקום למקום. למשל, R0 גבוה יותר בערים צפופות מאשר ביישובים חקלאיים.

(רוב כתבות החדשות - ואפילו חלק מהמאמרים האקדמיים! - מבלבלים בין R ל R0)

הערך של R0 לשפעת העונתית הוא בערך 1.288. זה אומר, שבתחילת התפרצות של שפעת, כל מדביק 1.28 אחרים בממוצע. (אם נשמע לכם מוזר שהמספר הזה הוא לא מספר שלם, לאמא הממוצעת בעולם יש 2.4 ילדים, ובישראל כ 3.2. זה לא אומר שמסתובבים ברחוב כל מני חצאי ילדים.)

מעריכים ש R0 ל COVID-19 הוא בערך 2.2,9 למרות שמחקר אחד לא סופי מעריך אותו ב !5.7(!) בווהאן.10

בסימולציה שלנו - בתחילת ההתפרצות, בממוצע - מדביק מישהו כל 4 ימים, למשך 10 ימים. “4 ימים” נכנס לתוך “10 ימים” פעמיים וחצי. זה אומר ש - בתחילת ההתפרצות, בממוצע - כל ידביק 2.5 אחרים. לכן R0 = 2.5. (הסתייגויות:11)

** שחקו עם מחשבון R0 הזה כדי לראות איך R0 מושפע מזמן ההחלמה והזמן להדבקות חדשות:**

אבל צריך לזכור, ככל שיש פחות , לוקח יותר זמן ל להפוך להיות . הערך של R תלוי עכשיו לא רק בערך הבסיסי שלו (R0) אלא גם בכמה אנשים כבר לא פגיעים (למשל, אנשים שהחלימו ופיתחו חסינות טבעית)

כשלמספיק אנשים יש חסינות, R < 1, והמגיפה נעצרת! המצב הזה נקרא חסינות עדר. במקרה של שפעת, חסינות עדר מושגת באמצעות חיסון. לנסות לתת לאנשים להידבק כדי להשיג “חסינות עדר טבעית” זה רעיון איום ונורא. (אבל אולי לא מהסיבות שאתם חושבים! תיכף נסביר.)

בואו נשחק שוב עם מודל SEIR, אבל הפעם נראה את R0, ערך R, והסף שממנו אנחנו משיגים חסינות עדר:

** שימו לב: המספר הכללי של המקרים לא מפסיק לעלות כשמגיעים לחסינות עדר. הוא ממשיך לטפס ** והוא חוצה את הסף של חסינות העדר בדיוק כשכמות המקרים מגיעה לשיא שלה. (ולא משנה איך תשנו את ההגדרות - נסו בעצמכם)

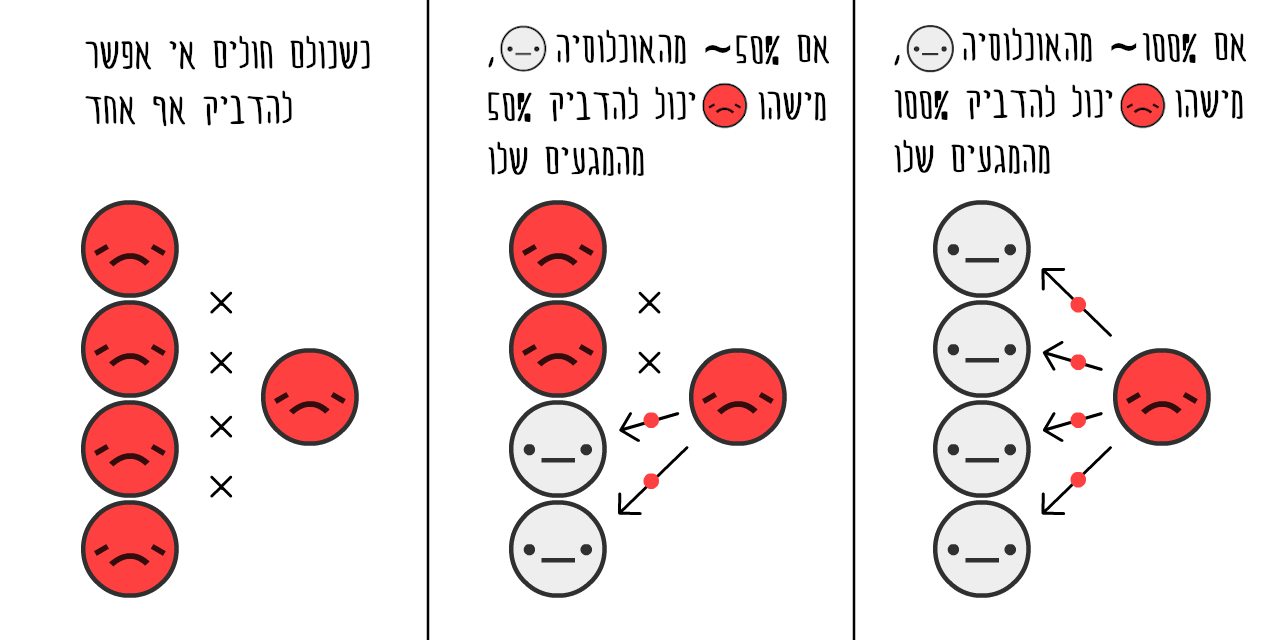
זה קורה בגלל שכשיש יותר אנשים שאינם מהכמות שדרושה לחסינות עדר, אנחנו מקבלים R < 1. וכש R < 1 כמות המקרים החדשים מפסיקה לגדול - וזה השיא.

אם תצאו מהמאמר הזה עם דבר אחד - הנה הדבר הזה - זו דיאגרמה מסובכת במיוחד אז קחו כמה דקות להפנים אותה:

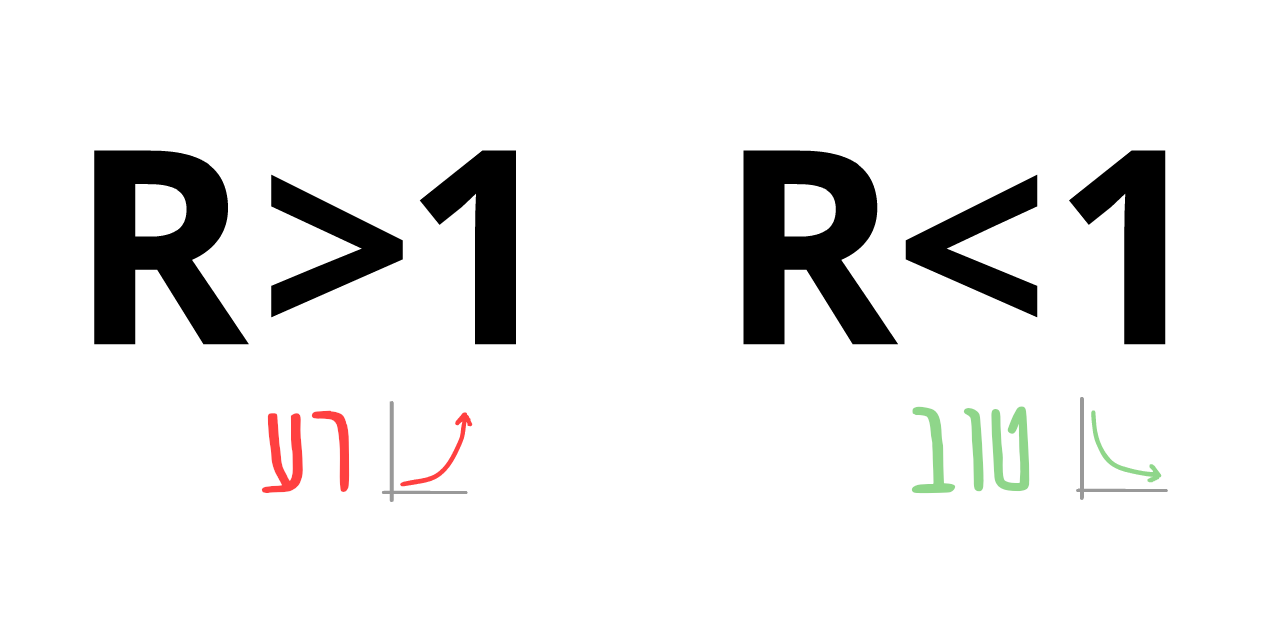
זה אומר שאנחנו לא חייבים לעצור את כל ההדבקות, או אפילו קרוב לזה, כדי לעצור את המגיפה!

זה מרגיש פרדוקסלי. COVID-19 היא מחלה מדבקת ביותר, אבל כדי לעצור אותה, אנחנו צריכים לעצור יותר מ 60% מההדבקות. 60% זה אולי לא ציון מרשים במיוחד בבית הספר אבל אם R0 = 2.5, ונצליח להקטין אותו ב 61% נקבל R = 0.975, וזה פחות מ 1, המגיפה נעצרה! (הנוסחא המדוייקת:12)

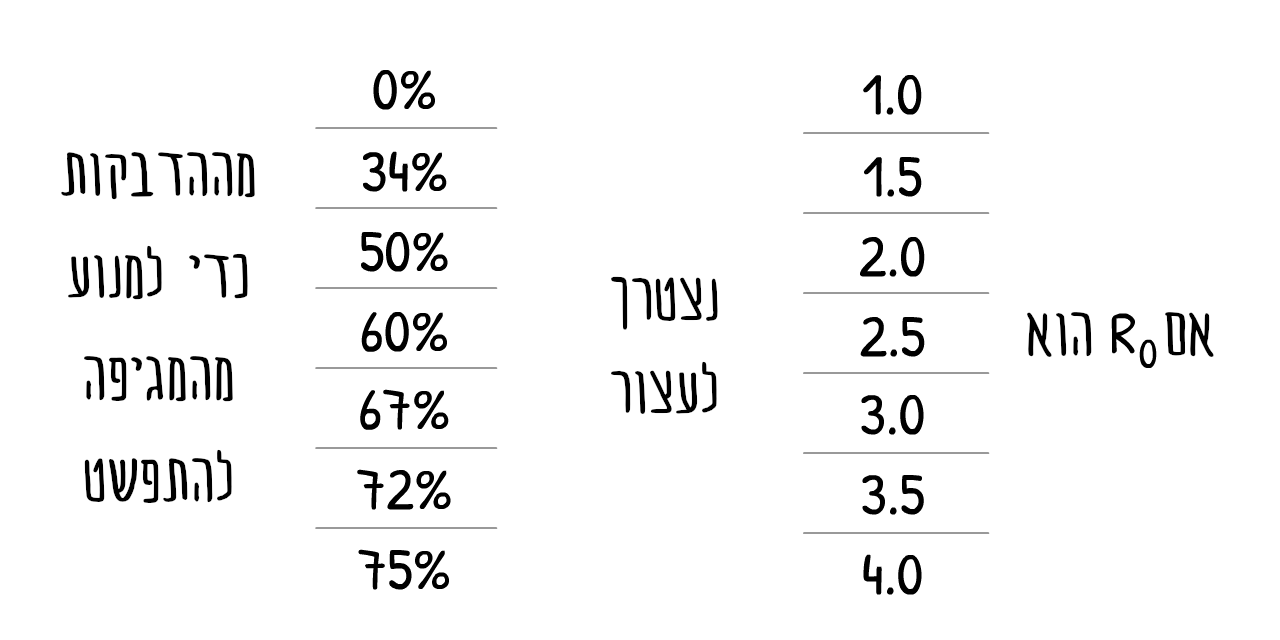
(אם נראה לכם שהערך של R0 או מספר אחר בסימולציה הזו נמוך/גבוה מדי, זה מצויין! בסוף המאמר יש סימולטור בוא תוכלו להזין את המספרים שלכם ולראות מה יוצא)

כל מה שאנחנו עושים כדי להתמודד עם המגיפה הזו - שטיפת ידיים, ריחוק חברתי, סגרים, בידוד, מעקב מגעים, מסיכות ואפילו “חסינות עדר” כולם מנסים להשיג אותה מטרה:

להגיע ל R < 1.

עכשיו, בואו נשתמש בסימולטור שלנו כדי לבדוק איך אנחנו יכולים להגיע ל R < 1 בדרך ששומרת על הבריאות הנפשית והפיננסית שלנו.

היכנו לנחיתת חירום…

החודשים הקרובים

…יכלו להיות יותר גרועים. הנה כמה יקומים מקבילים שלא הגענו אליהם:

תרחיש 0: לא לעשות שום דבר

בערך 1 מכל 20 נדבקים ב COVID-19 מגיע לטיפול נמרץ.13 במדינה עשירה כמו ארצות הברית, יש מיטת טיפול נמרץ אחת לכל 3,400 אנשים.14 לכן בארצות הברית אפשר לטפל במצב שבו 20 מכל 3,400 אנשים נדבקים - או 0.6% מהאוכלוסיה.

הנה מה שהיה קורה אם לא היינו עושים כלום, בהנחה שהיינו מגדילים את כמות המיטות ל 2% מהאוכלוסיה (יותר מפי 3):

לא טוב.

זה מה שגילה המחקר של אימפיריאל קולג’ מה-16 למרץ אם לא נעשה כלום יגמרו לנו המיטות במצב שבו 80% מהאוכלוסיה נדבקה.

אפילו אם רק 0.5% מהנדבקים מתים - הנחה נדיבה במצב שבו נגמרו המיטות בטיפול נמרץ - במדינה כמו ארצות הברית, עם 300 מיליון אנשים, 0.5% מתוך 80% מתוך 300 מיליון = 1.2 מיליון מתים…

(הרבה אתרי חדשות ופוסטים במדיה החברתית אומרים “80%” ידבקו בלי להוסיף את ההסתייגות: “אם לא נעשה כלום”. הופכים פחד לקליקים.)

תרחיש 1: משטחים את העקומה/חסינות עדר

התכנית “לשטח את העקומה” והתכנית הברטית של “חסינות עדר” היו בעצם אותה תכנית. הבריטים פשוט לא הסבירו אותה בצורה מוצלחת.15

שתי התכניות הללו סובלות מפגם קטלני.

קודם כל, בואו נסתכל על שתי הדרכים המרכזיות “לשטח את העקומה”: שטיפת ידיים וריחוק חברתי.

שטיפת ידיים מוגברת מורידה את התפשטות נגיפי השפעת בערך ב 25% במדינות מפותחות16, וסגר בלונדון הוריד את כמות המגעים הקרובים בערך ב 70%. בואו נניח ששטיפת ידיים יכולה לצמצם את R בעד 25%, וריחוק חברתי יכול לצמצם את R ב עד 1770%:

שחקו עם המחשבון הזה כדי לראות איך אחוז שטיפת היידים אצל אנשים שאינם , וריחוק חברתי מצמצמים את R: (החישוב הזה מציג את ההשפעה היחסית ולכן הגדלה של אחד הגורמים נראית כאילו היא מקטינה את האחרים.18)

בואו נבדוק מה היה קורה אם בתחילת מרץ 2020 היינו מגבירים את שטיפת הידיים אבל מפעילים רק ריחוק חברתי קל - כך ש R היה נמוך יותר אבל עדיין מעל 1:

שלוש הערות:

  1. הגישה הזו מפחיתה את סך כל המקרים! אפילו אם לא הצלחנו להגיע ל R < 1, הקטנת R עדיין מצילה חיים על ידי הפחתת כמות האנשים שיחלו מעבר לנקודה של חסינות עדר. הרבה אנשים חושבים שאם “נשטח את העקומה” נפזר את המקרים על יותר זמן אבל לא נקטין את סך הכל המקרים. זה לא נכון בשום מודל אפידימיולוגי.
  1. בזכות הריחוק המצומצם ושטיפת הידיים, מספר המקרים מגיע לשיא לפני הגעה לחסינות עדר. למעשה, מספר המקרים הכולל עובר את המספר שדרוש לחסינות עדר רק במעט! זו התכנית הבריטית! בנקודה הזו R < 1, אפשר להסיר את כל ההגבלות וההתפרצות לא תחזור!, תכנית מצויינת! למעט בעיה קטנה אחת…
  1. אנחנו עדיין עוברים את כמות במיטות בטיפול נמרץ. למשך כמה חודשים. (זכרו שהכפלנו את כמות המיטות פי שלוש לייתר ביטחון)

זה היה עוד ממצא של המחקר של אימפיריאל קולג’ מה 16 למרץ ששכנע את הבריטים לוותר על התכנית הזו. כל ניסיון “לשטח את העקומה” (להקטין את R אבל עדיין R > 1) ייכשל. הדרך היחידה היא “לשבור את העקומה”. (להקטין את R כך ש R < 1)

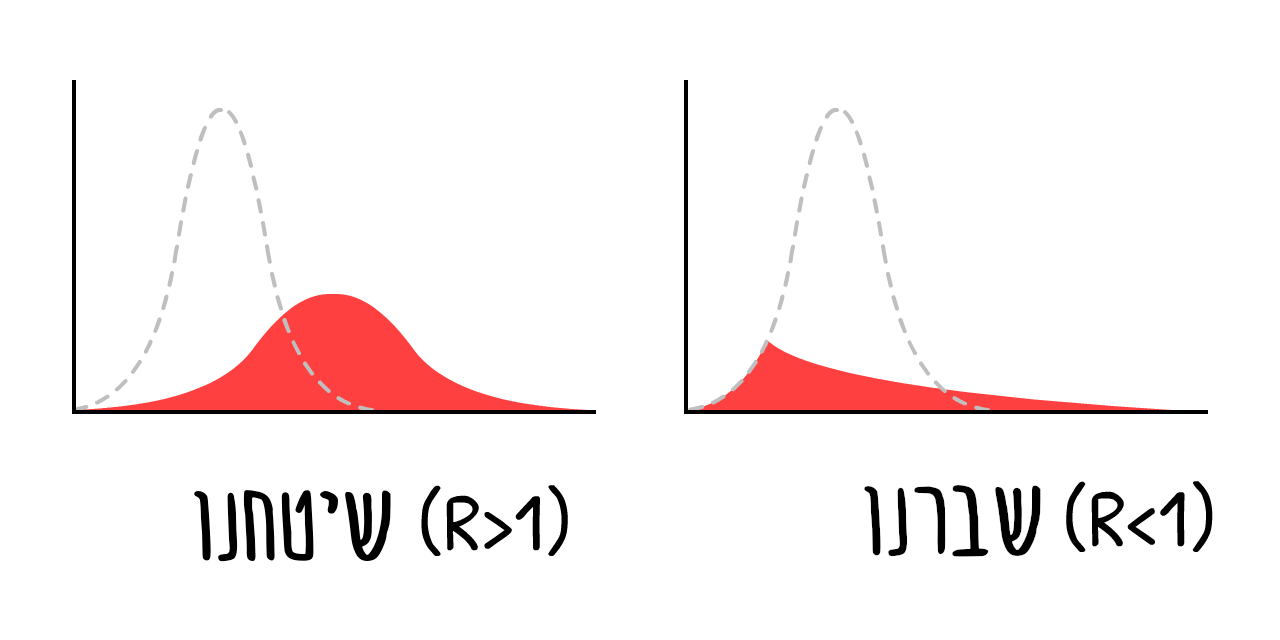
למשל…

תרחיש 2: סגר למשך כמה חודשים

בואו נראה מה קורה אם אנחנו “מרסקים” את העוקמה עם סגר של חמישה חודשים, מקטינים את כמעט לאפס ואז סוף סוף חוזרים לחיים נורמאליים:

אה…

זה “הגל השני” שכולם מדברים עליו. ברגע שאנחנו מסירים את הסגר, אנחנו מקבלים שוב R > 1. מספיק שישאר לנו אחד (או אחד שמגיע מחו"ל) כדי לגרום להתפרצות חמורה כמעט כמו תרחיש 0: לא עושים כלום.

סגר לא יכול להיות תרופה לבעיה. מה שהוא עושה זה “מאפס” את המצב ומחזיר אותנו לנקודת ההתחלה.

אז מה? סגר ועוד סגר ועד סגר עד אין סוף?

תרחיש 3: סגר לחלופין

התרחיש הזה הוצע במאמר של האימפריאל קולג’ מה 16 למרץ ושוב בנייר של הארוורד. 19

הנה הסימולציה: (אחרי שהתרחיש המוקלט יסתיים, תוכלו לקבוע את הפרמטרים שלכם וגם לשחק עם הנתונים תוך כדי שהסימולציה פועלת! אפשר גם לעצור ולהמשיך את הסימולטור ולשנות את המהירות)

הצלחנו לשמור את כמות המקרים החמורים מתחת לקיבולת של הטיפול הנמרץ! וזה הרבה יותר טוב מסגר של 18 חודשים עד שיהיה חיסון זמין. אנחנו צריכים רק… להטיל סגר לכמה חודשים, לפתוח לכמה חודשים, ולחזור על זה עד שיהיה חיסון זמין. (ואם לא יהיה חיסון זמין, עד שנגיע לחסינות עדר… ב 2022)

נחמד למתוח קווים של “קיבולת טיפול נמרץ” אבל יש עדיין כמה דברים שהסימולטור שלנו לא תופס. למשל:

בריאות נפשית: בדידות היא אחד מגורמי הסיכון לדיכאון, חרדה והתאבדויות, והיא קשורה למוות מוקדם כמו עישון של 15 סיגריות ליום.20

איתנות כלכלית: “מה עם הכלכלה” נשמע כאילו אכפת לך יותר מכמה גרושים מאשר מחיי אדם, אבל “הכלכלה” היא לא רק משחקים במניות: היא היכולת של אנשים לספק אוכל וקורת גג למשפחה שלהם, להשקיע בעתיד של הילדים שלהם, להינות מאומנות, אוכל ומשחקי מחשב - הדברים שמרכיבים את מה שאנחנו קוראים לו החיים שלנו. חוץ מזה, גם לעוני בעצמו יש השפעה נוראית על בריאות פיזית ונפשית.

זה לא אומר שלא נצטרך לעשות סגר שוב! נראה איך אפשר להשתמש בסגר בהמשך, אבל זה לא אידיאלי.

רגע… אבל טיוואן ודרום קוריאה הצליחו לעצור את התפשטות המגפה כבר 4 חודשים בלי סגר ארוך?

איך?

תרחיש 4: בדיקות, מעקב מגעים, בידודים

“יכולנו אולי לעשות מה שהם עשו מההתחלה אבל עכשיו מאוחר מדי. פספסנו את ההתחלה.”

אבל זה בדיוק העניין. “סגר לא פותר את הבעיה - הוא מחזיר אותנו לנקודת ההתחלה”… וזה בדיוק מה שאנחנו צריכים - לחזור לנקודת ההתחלה!

כדי להבין איך טיוואן וקוריאה הדרומית עצרו את התפשטות המגיפה, אנחנו צריכים להבין את לוח הזמנים של חולה COVID-19 טיפוסי21:

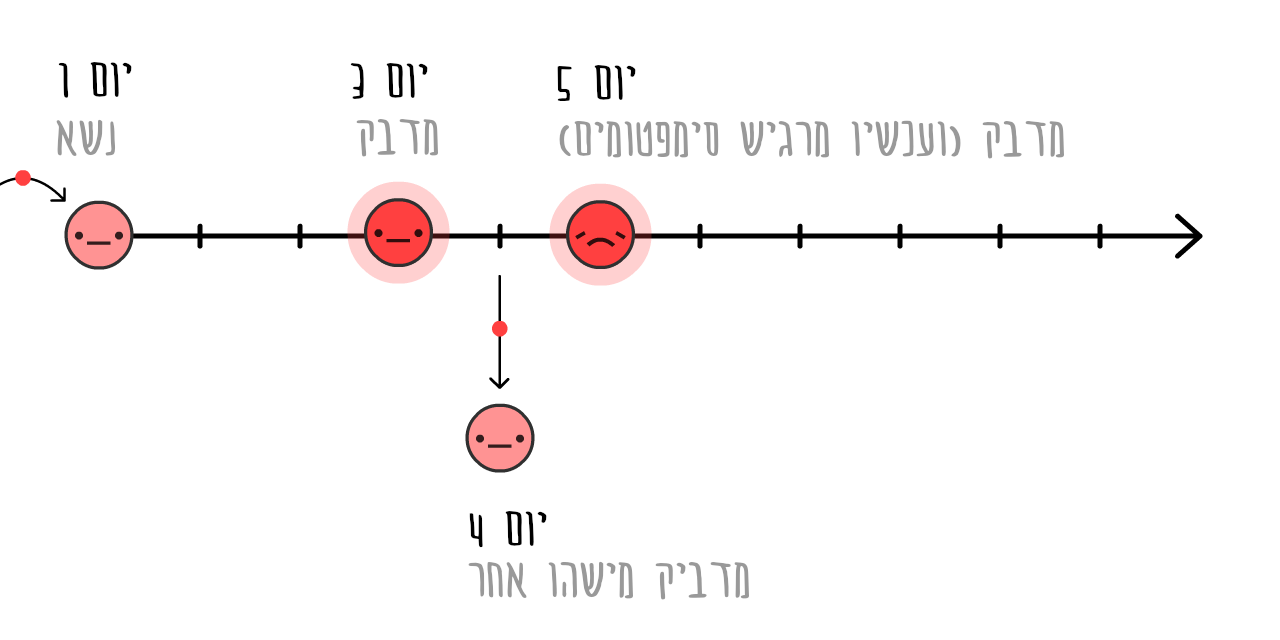
אם אנשים נכנסים לבידוד כשהם יודעים שהם חולים (כלומר מרגישים סימפטומים), הוירוס יכול להמשיך להתפשט:

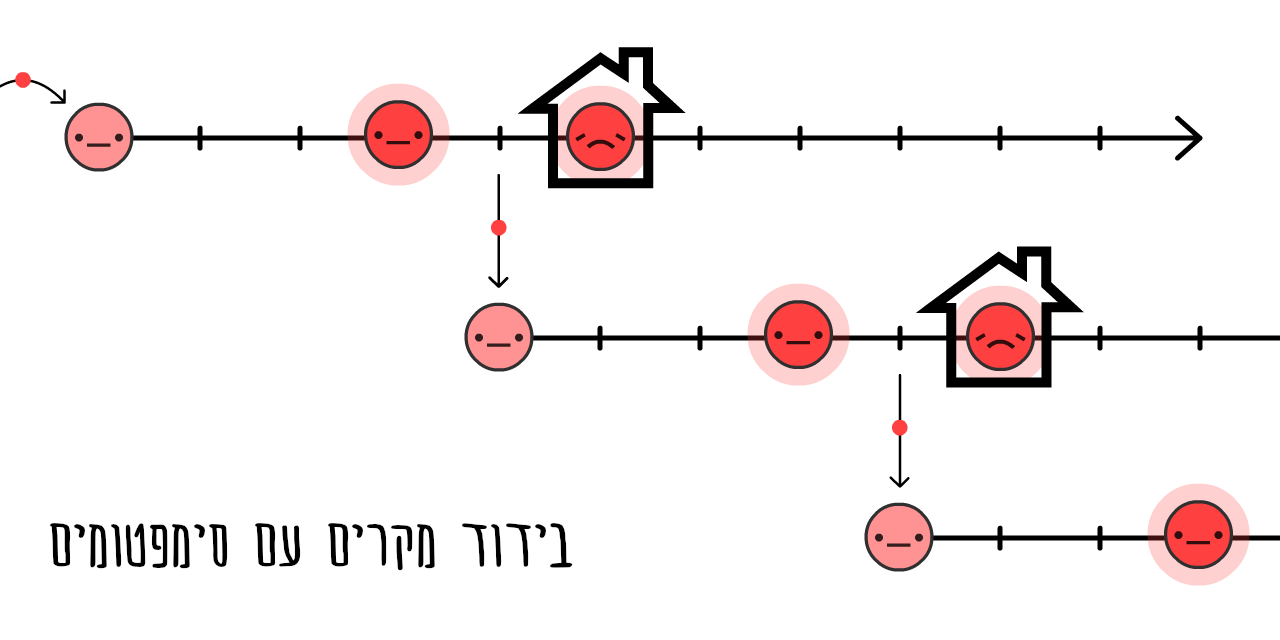
למעשה, 44% מכל ההדבקות הן הדבקות כאלו - פרה-סימפטומטיות! 22

אבל אם נמצא ונבודד את כל המגעים הקרובים של מי שפיתח סימפטומים… נהיה צעד אחד קדימה ונוכל לעצור את התפשטות המגפה.

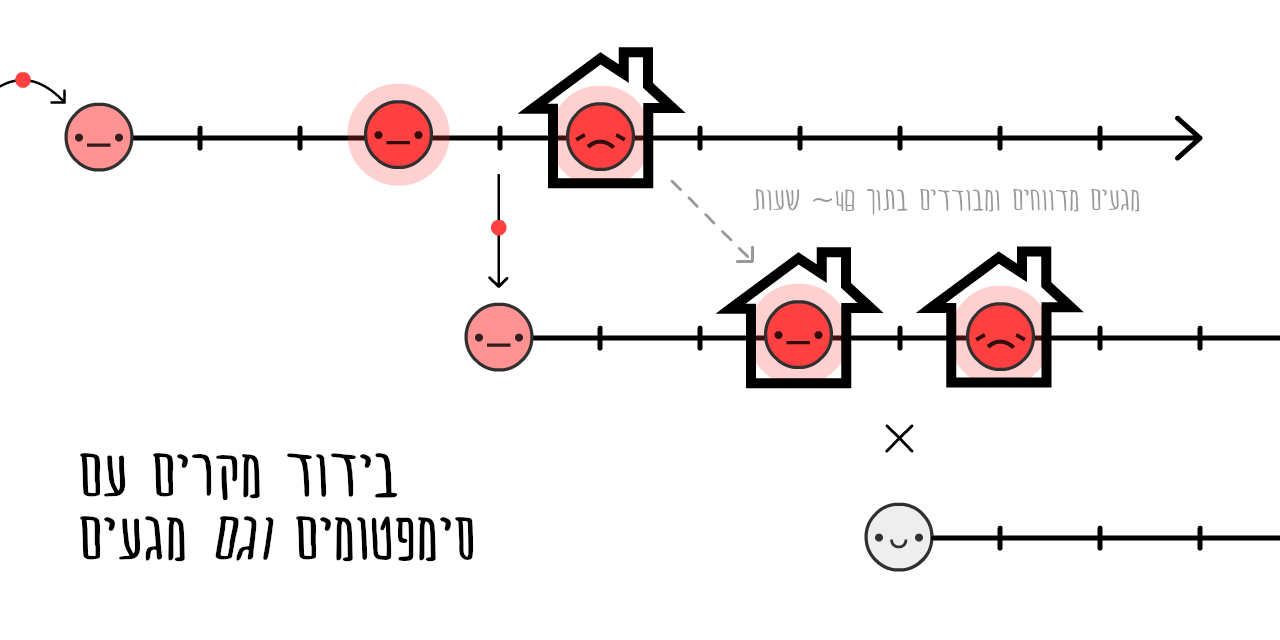
זה נקרא מעקב מגעים. זה רעיון שקיים כבר זמן ארוך, השתמשו בו כדי לעצור את התפרצות האבולה23, ועכשיו טיוואן וקוריאה הדרומית משתמשות בו כחלק ממלחמה שלהן במגיפה.

(השיטה הזו מאפשרת לנו גם להשתמש בבדיקות שיש לנו בצורה יעילה יותר ולמצוא חולים סמויים בלי סימפטומים בלי לבדוק את כל האוכלוסיה.)

בעבר, איתור מגעים נעשה באמצעות ראיונות עם חולים סימפטומטים אבל ראיונות כאלו איטיים מדי בשביל חלון ההדבקה של הקורונה (48 שעות) ולכן נדרשת עזרה של אפליקציות לאיתור מגעים.

(הרעיון של שימוש באפליקציות לאיתור מגעים לא בא מעולם ביטחון או ההיי טק הוא הוצע לראשונה על ידי צוות של אפידימיולוגים מאוקספורד.)

רגע, רגע, אפליקציות שרושמות עם מי הייתי במגע?… זה אומר לוותר לגמרי על הפרטיות שלי?

ממש לא! DP-3T, קבוצה של אפידימיולוגים ומומחי הצפנה (כולל אחד ממחברי המאמר הזה, Marchel Salathé) כבר עובדים על אפליקציה למעקב אחרי מגעים - שהקוד שלה פתוח לציבור - שלא חושפת את הזהות והמיקום שלך, מי היו המגעים שלך ואפילו לא כמה מגעים היו לך.

ככה זה עובד:

(& והנה הקומיקס המלא (באנגלית))

הפרוייקט הזה, ופרוייקטים דומים כמו TCN Protocol24 ו MIT PACT25, היוו השראה ל Google ו Apple להכניס איתור מגעים מבוסס פרטיות לתוך Android/iOS.26 (לא סומכים על גוגל ואפל? מעולה! היופי של המערכת הזו הוא שלא צריך לסמוך על אף אחד!) בקרוב ראשויות הבריאות יבקשו מכם להוריד אפליקציה. אם הקוד פתוח וזמין והיא מבוססת על הרעיונות האלו, הורידו אותה!

אבל מה עם אנשים שאין להם טלפון חכם? או הדבקות דרך ידיות של דלתות וכפתורים של מעליות? או מקרים שלא יפתחו סימפטומים בכלל? אפליקציות לאיתור מגעים לא יכולות לתפוס את כל ההדבקות… וזה בסדר גמור! אנחנו לא צריכים לתפוס את כל ההדבקות, רק 60% כדי לקבל R < 1.

בידוד חולים עם סימפטומים יכול להוריד את R ב עד 40%, ובידוד המגעים שלהם יכול להוריד את R ב עד 50%27:

לכן, אפילו אם לא נצליח לבודד 100% מהמגעים, אנחנו יכולים להגיע ל R < 1 בלי סגר! הרבה יותר טוב לבריאות הנפשית והכלכלית שלנו. (לגבי מי שצריך להיכנס לסגר/בידוד - הממשלות צריכות לתמוך בהם. ימי מחלה וכד’ יעלו הרבה פחות מסגרים חוזרים)

אנחנו שומרים על R < 1 עד שיש לנו חיסון שיכול להפוך אנשים חשופים ל אנשים חסינים. חיסון עדר בדרך הנכונה:

(שימו לב: המחשבון הזה מניח שחיסון יעיל ב 100%, בפועל נצטרך לחסן יותר אנשים כדי לקבל חסינות עדר.)

OK, בואו נראה, הנה סימולציה של:

  1. כמה חודשים של סגר, עד שנוכל…
  2. לעבור למעקב ובידוד של מגעים, עד שנוכל…
  3. לחסן מספיק אנשים ואז…
  4. ניצחנו.

זהו, ככה אנחנו מנחיתים את הסימולטור שלנו.

ככה ננצח את COVID-19.

…

אבל מה אם זה לא יעבוד כמו שאנחנו מקווים?

הפסימיסט ממציא את המצנח.

תרחיש 4+: נשף מסכות, קיץ, איפוסים

מה אם R0 הרבה יותר גדול ממה שהערכנו, וכל הצעדים שתוארו עד עכשיו, כולל הרחקה חברתית, עדיין לא מספיקים כדי להגיע ל R < 1?

שימו לב, בכל מקרה הקטנה של R מקטינה את כמות המקרים הכללית ולכן חוסכת חיי אדם. אבל R < 1 היא עדיין המטרה שלנו לכן הנה עוד כמה צעדים להקטנת R:

נשף מסכות:

“רגע,” אתם אומרים, “חשבתי שמסכות לא מונעות ממך להדבק?”

נכון. מסכות לא מונעות ממך להדבק28… הן מונעות ממך להדביק אחרים.

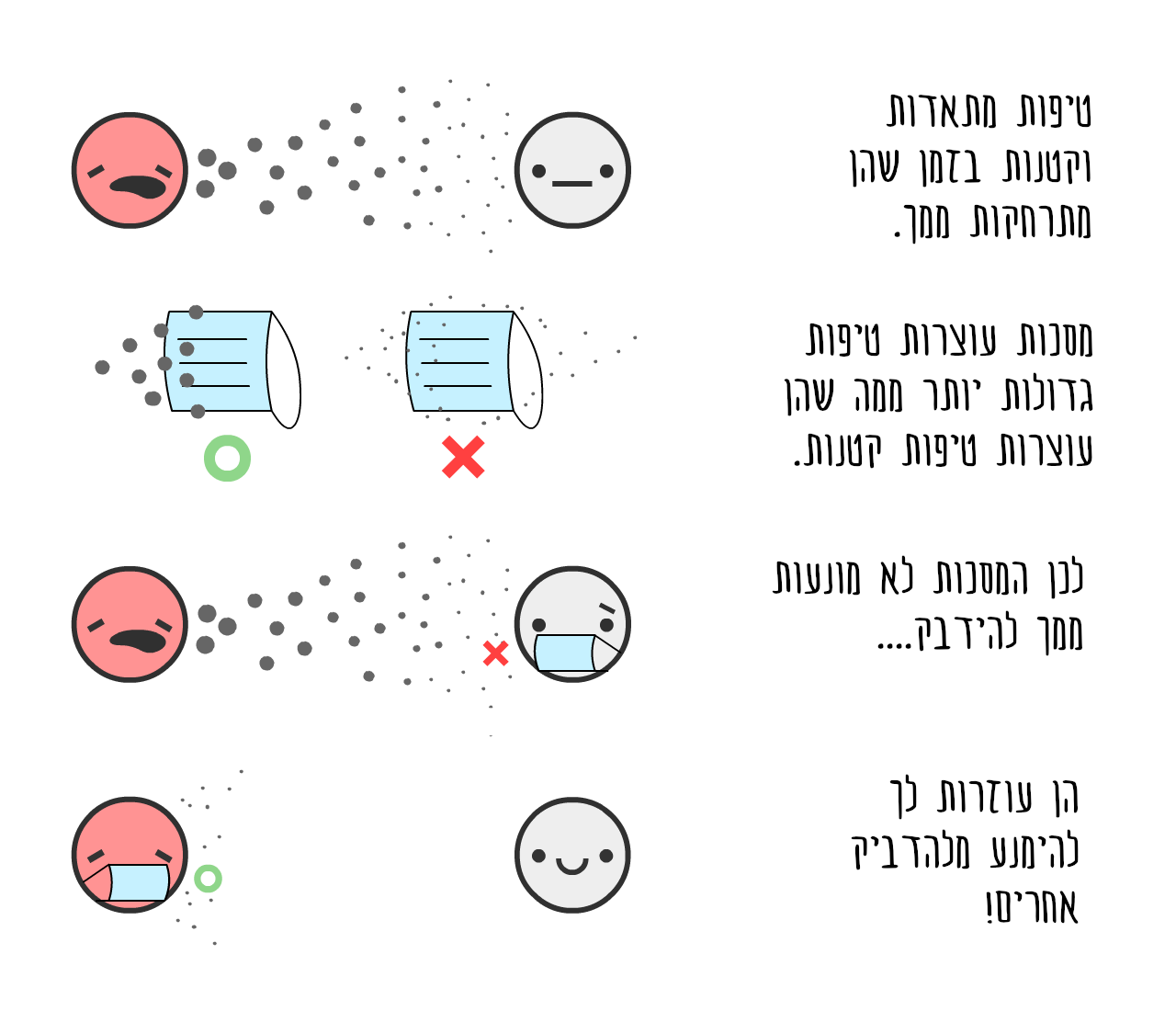
או במספרים: מסיכה על אדם חולה מקטינה את נגיפי השפעת ברסס ב 70%.29 הקטנה של 70% בהדבקה שקולה להשפעה של סגר!

על כל פנים, אנחנו עדיין לא יודעים מה ההשפעה הספציפית של מסכות על COVID-19. במחקרים מדעיים מקובל לפרסם תוצאות רק בביטחון של 95% (מקובל…30) נכון ל1 במאי 2020 מסכות עדיין לא וודאיות ב 95%.

בכל מקרה, פנדמיות הן כמו משחק פוקר. אם תהמר רק כשאתה בטוח ב 95% תפסיד בכל משחק. כמו שמציין מאמר על מסכות ב British Medical Journal,31 אנחנו חייבים לעשות ניתוחים של עלות/תועלת בתנאים של אי-וודאות. ולכן:

עלות: אם מסכות בד ביתיות (ביעילות של 2/3~ ממסכות מנתחים 32), זולות מאד. אם מסכות מנתחים יותר יקרות אבל עדיין זולות למדי.

תועלת: אפילו אם יש סיכוי של 50-50 שמסכות מקטינות את שיעור ההדבקה ב 0% או ב 70%, ממוצע התוחלת הוא עדיין 35%, כמו חצי סגר! אז בואו נניח שההשפעה היא 35% כפיצוי על אי הוודאות שלנו. (שוב, שחקו עם המספרים ובידקו את התסריט שלכם)

קשה לחבוש מסיכות נכון. קשה גם לשטוף ידיים לפי ההנחיות של משרד הבריאות אבל אנחנו עדיין עושים את זה, בגלל ששטיפת ידיים לא מושלמת עדיפה על כלום.

אנשים יחבשו מסיכות ויזלזלו בשטיפת ידיים ובריחוק חברתי. כן, וחגורות בטיחות גורמות לאנשים להתעלם משלטי עצור, וצחצוח שיניים גורם לאנשים לאכול אבנים. אבל ברצינות, לדעתנו ההפך הוא הנכון: מסכות הן תזכורת קבועה למצב ולזהירות שצריך להפגין. במזרח אסיה המסכות הן סמל לסודלידריות.

מסכות לבדן לא יביאו אותנו ל R < 1. אבל אם שטיפת ידים ובידוד מגעים יבאו אותנו ל R = 1.10, אפילו אם רק שליש מהאנשים יחבשו מסכות הם יעבירו אותנו מעבר ל R < 1, המגיפה נעצרה!

(עוד טיעונים בעד ונגד מסכות:33)

קיץ:

OK, קיץ זה לא משהו שאנחנו יכולים לעשות, אבל הקיץ יעזור! חלק מאתרי החדשות מדווחים שהקיץ לא יעשה כלום ל COVID-19. הם חצי צודקים: הקיץ לא יגרום ל R < 1 אבל הוא יוריד את R.

עבור COVID-19, כל עליה של 1° מביאה לירידה של 1.2% ב R34. הפרש הטמפרטורות בין הקיץ לחורף בישראל הוא בערך 10° ולכן אנחנו יכולים לצפות לירידה של 12% ב R.

הקיץ לבדו לא יביא ל R < 1 אבל אם יש לנו אמצעים מוגבלים, אנחנו יכולים לשחרר חלק מההגבלות בקיץ ולהחזיר אותן בחורף.

איפוסים:

ואם כל זה עדיין לא מספיק, אנחנו יכולים לעשות עוד סגר.

אבל בגלל ש R כבר מוקטן בכל מני צורות אחרות לא נצטרך לעשות חודש חופשי וחודשיים סגר במעגל אין סופי. נצטרך אולי עוד סגר או שניים עד שיהיה חיסון זמין. (סינגפור נאלצה לעשות סגר שני לאחרונה אחרי 4 חודשים של שליטה במגיפה. זה לא כישלון: ככה נראית מלחמה מוצלחת בנגיף)

הנה סימולציה של תרחיש מעורב כזה:

  1. סגר, ואז
  2. קצת הגיינה משופרת, עם קצת איתור מגעים, עם קצת מסכות ואז…
  3. עוד סגר לאיפוס לפני שנמצא החיסון

וזה בלי לדבר על שאר הדברים שאנחנו יכולים לעשות כדי להנמיך את R:

. . .

אנחנו מקווים שהתכנית הזו נותנת לכם תקווה.

גם תחת ההנחות הפסימיות יותר, אפשר לנצח את המגפה הזו ולשמור על הבריאות הנפשית והכלכלית שלנו. נשתמש בסגר כדי לאפס את המצב כשנצטרך, נשמור על R < 1 עם בידוד מקרים + מעקב מגעים ששומר על הפרטיות שלנו + מסכות לכולנו… והחיים יכולים לחזור ל(סוג של) מסלולם.

אז נסבול מידיים יבשות. אבל נוכל לצאת לבלות בין הירקות ברמי לוי, נוכל ללכת לקולנוע לראות את הלהיט התורן, נוכל להמשיך לחיות את החיים שלנו.

גם בתרחישים הקשים יותר… החיים ממשיכים.

אז עכשיו, בואו נתכנן כמה תרחישים עוד יותר גרועים:

השנים הקרובות

חטפתם COVID-19 והבראתם או שקיבלתם חיסון. ברכות! עכשיו אתם מחוסנים.

…לכמה זמן?

לגבי בני אדם, נכון ל 1 במאי 2020, “לכמה זמן?” היא שאלה פתוחה.

לסימולציה הבאה נניח שאנחנו חסינים לשנה.

הנה סימולציה שמתחילה ב 100% , דועכת אקספוננציאלית לאנשים חשופים ללא חסינות אחרי שנה:

שובה של הדעיכה האקספוננציאלית.

זה הSERIRS Model. ה S שנוספה בסוף היא אנשים שחוזרים להיות פגיעים Susceptible.

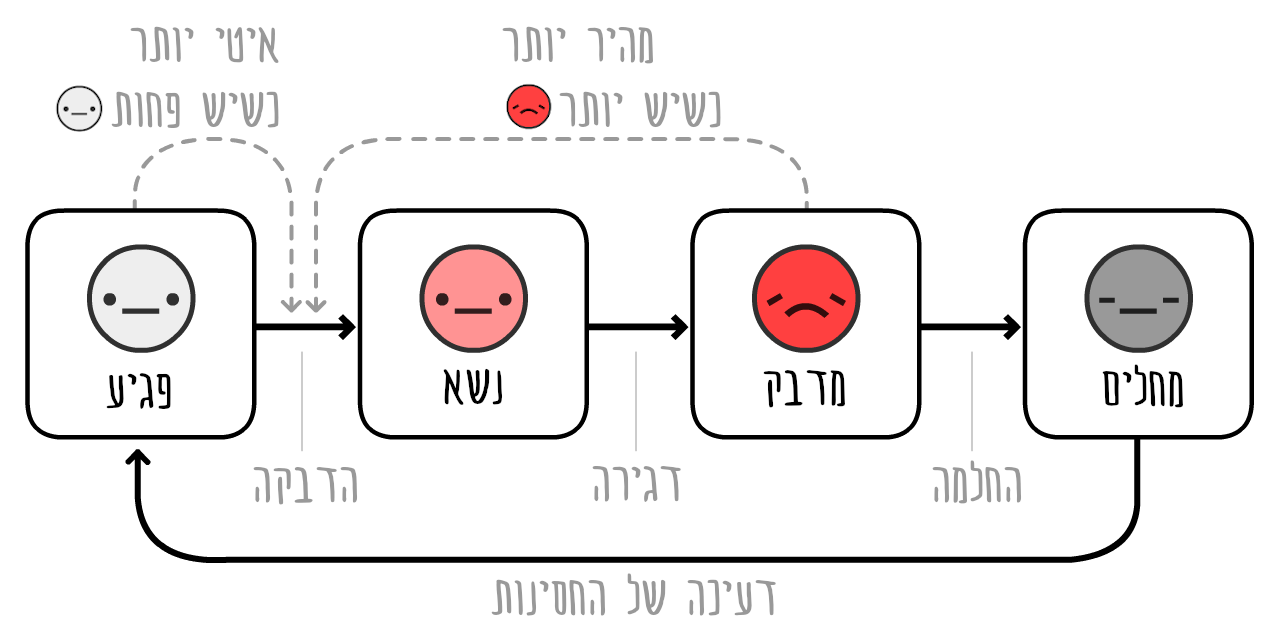
בואו נעשה סימולציה של התפרצות COVID-19 בלי שום התערבות… בהנחה שהחסינות מחזיקה מעמד שנה אחת:

בסימולציות הקודמות היה לנו רק שיא אחד שעבר את הקיבולת של מערכת בטיפול הנמרץ. עכשיו יש לנו כמה כאלו ו מתייצבים באופן קבוע על שיא הקיבולת של הטיפול הנמרץ. (שאותו הכפלנו פי שלוש כזכור)

R = 1, היא כאן להישאר.

למרבה המזל, בגלל שהקיץ מפחית את R, המצב ישתפר:

אוי.

הקיץ מחריף את הקפיצות וגם גורם להן לחזור בקביעות! זה קורה בגלל שהקיץ מפחית את החדשים, אבל אז גורם גם לירידה בכמות המחוסנים החדשים ולכן החסינות יורדת בקיץ וגורמת לקפיצה קבועה בחורף.

למרבה המזל, הפיתרון לזה פשוט - לחסן בכל סתיו/חורף, כמו שאנחנו עושים עכשיו עם השפעת:

(אחרי שתפעילו את ההקלטה נסו לעשות סימולציה של קמפיין החיסונים שלכם! אפשר לעצור ולהמשיך את הסימולציה מתי שרוצים)

אבל הנה השאלה המפחידה יותר:

מה אם לא יהיה חיסון במשך שנים? או לעולם?

רק להבהיר: זה לא תרחיש סביר. מרבית האפידימיולוגים מצפים לחיסון בתוך שנה או שנתיים. נכון שלא נמצא עד היום חיסון לאף נגיף ממשפחת הקורונה אבל זה בגלל שמגפת ה SARS נעצרה מהר ונגיף ההצטננות לא היה שווה את ההשקעה.

ועדיין, מומחים הביעו דאגות: מה אם לא נצליח לייצר מספיק?39 מה אם נעשה את זה בחיפזון, והחיסון לא יהיה בטוח?40

אפילו אם נמצא את עצמנו בסיוט של “אין-חיסון”, עדיין יהיו לנו שלושה קרשי הצלה:

  1. נעשה סדרה של צעדים להקטנת R שלא יהיו קשים מדי עד שנגיע לחסינות עדר. (זה יגמר בהרבה מתים ונזק לריאות, ולא יעבוד אם יתברר שהחסינות עוברת מהר)
  1. נמשיך לעשות צעדים להקטנת R לנצח. מסיכות ובידוד מגעים יהיו חלק מהחיים בעידן שאחרי COVID-19.
  1. נעשה צעדים להקטנת R עד שנצליח לפתח טיפול שיגרום ל COVID-19 להיות מחלה שלא גורמת לכל כך הרבה טיפול נמרץ. (את זה אנחנו צריכים לעשות בכל מקרה) הקטנת היקף האישפוזים פי 10 שקולה להגדלת כמות מיטת טיפול נמרץ פי 10.

הנה סימולציה שמניחה שאין חסינות ארוכת טווח, אין חיסון, ואין אפילו צעדי מניעה. רק הגדלה הדרגתית של קיבולת טיפול נמרץ כדי להתמודד עם השיאים

גם במקרה הכי גרוע הזה… החיים ממשיכים.

. . .

אולי תרצו לנסות הנחות אחרות או לבדוק את את הדרך שלכם לצאת מהמצב הזה.

הנה סימולציה שבה תוכלו לשחק בכל המספרים!

הסימולטור הבסיסי הזה לימוד אותנו כמה דברים, וענה לנו על כמה שאלות לגבי החודשים האחרונים, החודשים הקרובים והשנים הבאות.

אז בואו נחזור ל…

עכשיו

המטוס שקע, אנחנו על הרפסודה המתנפחת. הגיע הזמן למצוא יבשה.41

צוותים של קובעי מדינות ואפידימיולוגים הגיעו להסכמה לגבי הדרך שבה נביס את COVID-19 תוך כדי שמירה על החיים שלנו ועל החרויות שלנו.

הנה התמצית:

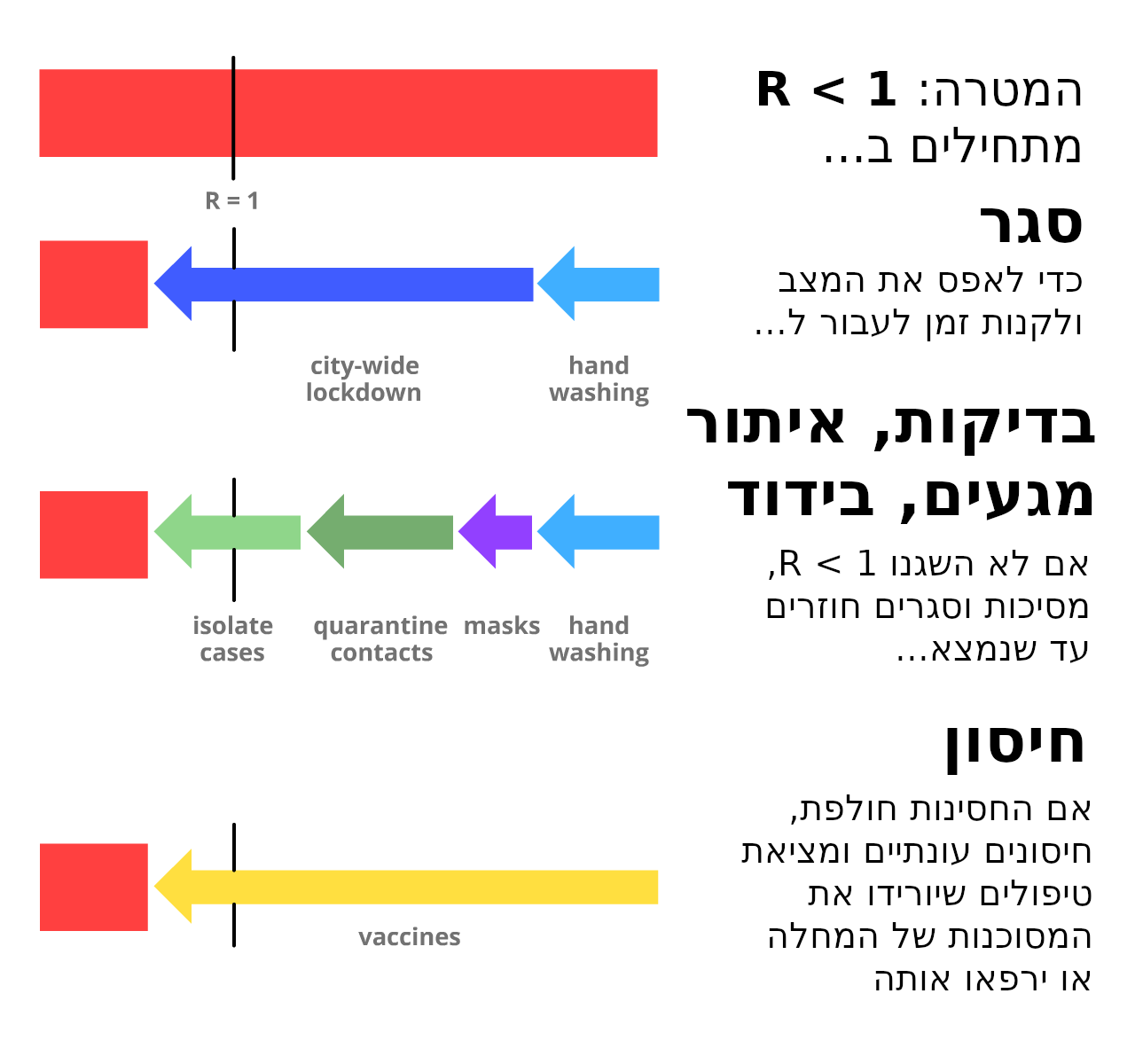
אז מה כל זה אומר בשבילנו עכשיו?

לכולם: לכבד את הסגר כדי שנוכל לצאת מהשלב הראשון במהירות. להמשיך לשטוף ידיים. לחבוש מסיכות. להוריד את האפליקציות לאיתור מגעים כשיהיו מוכנות. לשמור על הבריאות, נפשית וגופנית!

לקובעי מדיניות: דאגו לתמיכה באנשים שנאלצים להיות בבידוד. דאגו למעקב אחרי מגעים באמצעות אפליקציות רלוונטיות. עודדו השקעה בדברים שצריך לפתח כמו…

לאנשים שבונים דברים: אנחנו צריכים בדיקות, מכשירי הנשמה, ציוד מיגון אישי לבתי החולים, חיסונים, אפליקציות בידוד, טיפולים שאינם חיסונים, עוד בדיקות ועוד בדיקות ותקווה.

לא לפחד כלל זה קצת הרבה, עדיף לפחד קצת ולחצות את הגשר הצר באופטימיות.

  1. These footnotes will have sources, links, or bonus commentary. Like this commentary!

    This guide was published on May 1st, 2020. Many details will become outdated, but we’re confident this guide will cover 95% of possible futures, and that Epidemiology 101 will remain forever useful.↩

  2. “The mean [serial] interval was 3.96 days (95% CI 3.53–4.39 days)”. Du Z, Xu X, Wu Y, Wang L, Cowling BJ, Ancel Meyers L (Disclaimer: Early release articles are not considered as final versions)↩

  3. Remember: all these simulations are super simplified, for educational purposes.

    One simplification: When you tell this simulation “Infect 1 new person every X days”, it’s actually increasing # of infected by 1/X each day. Same for future settings in these simulations – “Recover every X days” is actually reducing # of infected by 1/X each day.

    Those aren’t exactly the same, but it’s close enough, and for educational purposes it’s less opaque than setting the transmission/recovery rates directly.↩

  4. “The median communicable period […] was 9.5 days.” Hu, Z., Song, C., Xu, C. et al Yes, we know “median” is not the same as “average”. For simplified educational purposes, close enough.↩

  5. For more technical explanations of the SIR Model, see the Institute for Disease Modeling and Wikipedia↩

  6. For more technical explanations of the SEIR Model, see the Institute for Disease Modeling and Wikipedia↩

  7. “Assuming an incubation period distribution of mean 5.2 days from a separate study of early COVID-19 cases, we inferred that infectiousness started from 2.3 days (95% CI, 0.8–3.0 days) before symptom onset” (translation: Assuming symptoms start at 5 days, infectiousness starts 2 days before = Infectiousness starts at 3 days) He, X., Lau, E.H.Y., Wu, P. et al.↩

  8. “The median R value for seasonal influenza was 1.28 (IQR: 1.19–1.37)” Biggerstaff, M., Cauchemez, S., Reed, C. et al.↩

  9. “We estimated the basic reproduction number R0 of 2019-nCoV to be around 2.2 (90% high density interval: 1.4–3.8)” Riou J, Althaus CL.↩

  10. “we calculated a median R0 value of 5.7 (95% CI 3.8–8.9)” Sanche S, Lin YT, Xu C, Romero-Severson E, Hengartner N, Ke R.↩

  11. This is pretending that you’re equally infectious all throughout your “infectious period”. Again, simplifications for educational purposes.↩

  12. Remember R = R0 * the ratio of transmissions still allowed. Remember also that ratio of transmissions allowed = 1 - ratio of transmissions stopped.

    Therefore, to get R < 1, you need to get R0 * TransmissionsAllowed < 1.

    Therefore, TransmissionsAllowed < 1/R0

    Therefore, 1 - TransmissionsStopped < 1/R0

    Therefore, TransmissionsStopped > 1 - 1/R0

    Therefore, you need to stop more than 1 - 1/R0 of transmissions to get R < 1 and contain the virus!↩

  13. “Percentage of COVID-19 cases in the United States from February 12 to March 16, 2020 that required intensive care unit (ICU) admission, by age group”. Between 4.9% to 11.5% of all COVID-19 cases required ICU. Generously picking the lower range, that’s 5% or 1 in 20. Note that this total is specific to the US’s age structure, and will be higher in countries with older populations, lower in countries with younger populations.↩

  14. “Number of ICU beds = 96,596”. From the Society of Critical Care Medicine USA Population was 328,200,000 in 2019. 96,596 out of 328,200,000 = roughly 1 in 3400.↩

  15. “He says that the actual goal is the same as that of other countries: flatten the curve by staggering the onset of infections. As a consequence, the nation may achieve herd immunity; it’s a side effect, not an aim. […] The government’s actual coronavirus action plan, available online, doesn’t mention herd immunity at all.”

    From a The Atlantic article by Ed Yong↩

  16. “All eight eligible studies reported that handwashing lowered risks of respiratory infection, with risk reductions ranging from 6% to 44% [pooled value 24% (95% CI 6–40%)].” We rounded up the pooled value to 25% in these simulations for simplicity. Rabie, T. and Curtis, V. Note: as this meta-analysis points out, the quality of studies for handwashing (at least in high-income countries) are awful.↩

  17. “We found a 73% reduction in the average daily number of contacts observed per participant. This would be sufficient to reduce R0 from a value from 2.6 before the lockdown to 0.62 (0.37 - 0.89) during the lockdown”. We rounded it down to 70% in these simulations for simplicity. Jarvis and Zandvoort et al↩

  18. This distortion would go away if we plotted R on a logarithmic scale… but then we’d have to explain logarithmic scales.↩

  19. “Absent other interventions, a key metric for the success of social distancing is whether critical care capacities are exceeded. To avoid this, prolonged or intermittent social distancing may be necessary into 2022.” Kissler and Tedijanto et al↩

  20. See Figure 6 from Holt-Lunstad & Smith 2010. Of course, big disclaimer that they found a correlation. But unless you want to try randomly assigning people to be lonely for life, observational evidence is all you’re gonna get.↩

  21. 3 days on average to infectiousness: “Assuming an incubation period distribution of mean 5.2 days from a separate study of early COVID-19 cases, we inferred that infectiousness started from 2.3 days (95% CI, 0.8–3.0 days) before symptom onset” (translation: Assuming symptoms start at 5 days, infectiousness starts 2 days before = Infectiousness starts at 3 days) He, X., Lau, E.H.Y., Wu, P. et al.

    4 days on average to infecting someone else: “The mean [serial] interval was 3.96 days (95% CI 3.53–4.39 days)” Du Z, Xu X, Wu Y, Wang L, Cowling BJ, Ancel Meyers L

    5 days on average to feeling symptoms: “The median incubation period was estimated to be 5.1 days (95% CI, 4.5 to 5.8 days)” Lauer SA, Grantz KH, Bi Q, et al↩

  22. “We estimated that 44% (95% confidence interval, 25–69%) of secondary cases were infected during the index cases’ presymptomatic stage” He, X., Lau, E.H.Y., Wu, P. et al↩

  23. “Contact tracing was a critical intervention in Liberia and represented one of the largest contact tracing efforts during an epidemic in history.” Swanson KC, Altare C, Wesseh CS, et al.↩

  24. Temporary Contact Numbers, a decentralized, privacy-first contact tracing protocol↩

  25. PACT: Private Automated Contact Tracing↩

  26. Apple and Google partner on COVID-19 contact tracing technology. Note they’re not making the apps themselves, just creating the systems that will support those apps.↩

  27. From the same Oxford study that first recommended apps to fight COVID-19: Luca Ferretti & Chris Wymant et al See Figure 2. Assuming R0 = 2.0, they found that:

    • Symptomatics contribute R = 0.8 (40%)
    • Pre-symptomatics contribute R = 0.9 (45%)
    • Asymptomatics contribute R = 0.1 (5%, though their model has uncertainty and it could be much lower)
    • Environmental stuff like doorknobs contribute R = 0.2 (10%)

    And add up the pre- & a-symptomatic contacts (45% + 5%) and you get 50% of R!↩

  28. “None of these surgical masks exhibited adequate filter performance and facial fit characteristics to be considered respiratory protection devices.” Tara Oberg & Lisa M. Brosseau↩

  29. “The overall 3.4 fold reduction [70% reduction] in aerosol copy numbers we observed combined with a nearly complete elimination of large droplet spray demonstrated by Johnson et al. suggests that surgical masks worn by infected persons could have a clinically significant impact on transmission.” Milton DK, Fabian MP, Cowling BJ, Grantham ML, McDevitt JJ↩

  30. Any actual scientist who read that last sentence is probably laugh-crying right now. See: p-hacking, the replication crisis)↩

  31. “It is time to apply the precautionary principle” Trisha Greenhalgh et al [PDF]↩

  32. Davies, A., Thompson, K., Giri, K., Kafatos, G., Walker, J., & Bennett, A See Table 1: a 100% cotton T-shirt has around 2/3 the filtration efficiency as a surgical mask, for the two bacterial aerosols they tested.↩

  33. “We need to save supplies for hospitals.” Absolutely agreed. But that’s more of an argument for increasing mask production, not rationing. In the meantime, we can make cloth masks.↩

  34. “One-degree Celsius increase in temperature […] lower[s] R by 0.0225” and “The average R-value of these 100 cities is 1.83”. 0.0225 ÷ 1.83 = ~1.2%. Wang, Jingyuan and Tang, Ke and Feng, Kai and Lv, Weifeng↩

  35. “SARS-specific antibodies were maintained for an average of 2 years […] Thus, SARS patients might be susceptible to reinfection ≥3 years after initial exposure.” Wu LP, Wang NC, Chang YH, et al. “Sadly” we’ll never know how long SARS immunity would have really lasted, since we eradicated it so quickly.↩

  36. “We found no significant difference between the probability of testing positive at least once and the probability of a recurrence for the beta-coronaviruses HKU1 and OC43 at 34 weeks after enrollment/first infection.” Marta Galanti & Jeffrey Shaman (PDF)↩

  37. “Once a person fights off a virus, viral particles tend to linger for some time. These cannot cause infections, but they can trigger a positive test.” from STAT News by Andrew Joseph↩

  38. From Bao et al. Disclaimer: This article is a preprint and has not been certified by peer review (yet). Also, to emphasize: they only tested re-infection 28 days later.↩

  39. “If a coronavirus vaccine arrives, can the world make enough?” by Roxanne Khamsi, on Nature↩

  40. “Don’t rush to deploy COVID-19 vaccines and drugs without sufficient safety guarantees” by Shibo Jiang, on Nature↩

  41. Dry land metaphor from Marc Lipsitch & Yonatan Grad, on STAT News↩

(Click to show Feetnotes)

Feetnotes:

wash your hands! 👏 v.49